Exact kernel feature basis — b

Generates a design matrix that exactly represents a provided kernel, so that the Gram matrix is equal to the kernel matrix. The feature map is $$ \phi(x') = K_{x,x}^{-1/2} k_{x,x'}, $$ where $K_{x,x}$ is the kernel matrix for the data points $x$ and $k_{x, x'}$ is the vector of kernel function evaluations at the data points and the new value. While exact, this function is not particularly computationally efficient. Both fitting and prediction require backsolving the Cholesky decomposition of the kernel matrix for the original data points.

Usage

b_ker(
  ...,
  kernel = k_rbf(),
  stdize = c("scale", "box", "symbox", "none"),
  x = NULL,
  shift = NULL,
  scale = NULL
)

Arguments

...: The variable(s) to build features for. A single data frame or matrix may be provided as well. Missing values are not allowed.
kernel: A kernel function. If one of the recognized kernel functions such as k_rbf() is provided, then the computations will be exact. Otherwise, the fast Fourier transform of the provided kernel function is used to generate the random features. The kernel should be shift-invariant and decay to zero at positive and negative infinity.
stdize: How to standardize the predictors, if at all. The default "scale" applies scale() to the input so that the features have mean zero and unit variance, "box" scales the data along each dimension to lie in the unit hypercube, and "symbox" scales the data along each dimension to lie in $[-0.5, 0.5]^d$.
x: The (training) data points at which to evaluate the kernel. If provided, overrides ....
shift: Vector of shifts, or single shift value, to use. If provided, overrides those calculated according to stdize.
scale: Vector of scales, or single scale value, to use. If provided, overrides those calculated according to stdize.

Value

A matrix of kernel features.

Examples

data(quakes)

# exact kernel ridge regression
k = k_rbf(0.1)
m = ridge(depth ~ b_ker(lat, long, kernel = k), quakes)
cor(fitted(m), quakes$depth)^2
#> [1] 0.9668987

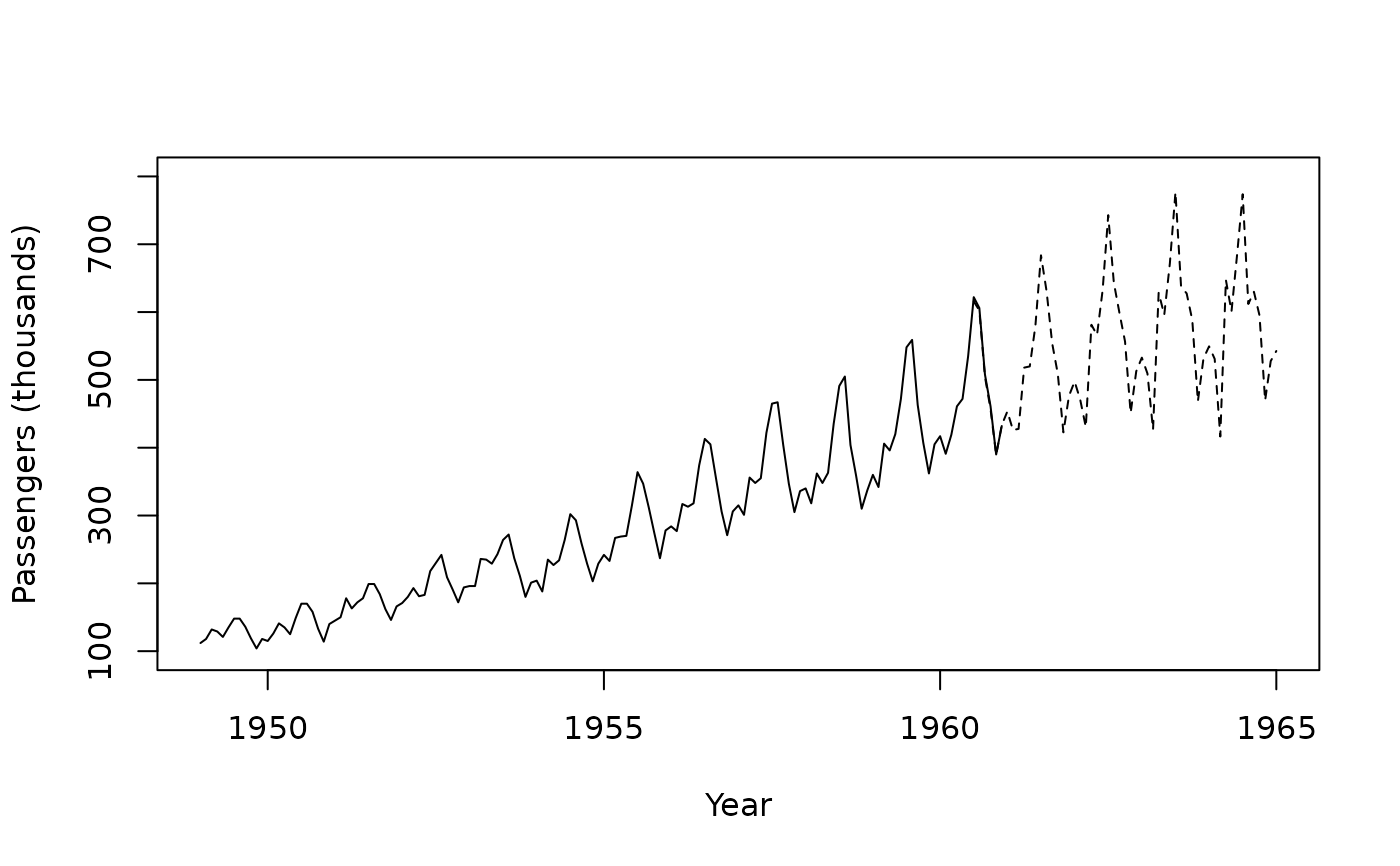
# Forecasting example involving combined kernels
data(AirPassengers)
x = seq(1949, 1961 - 1/12, 1/12)
y = as.numeric(AirPassengers)
x_pred = seq(1961 - 1/2, 1965, 1/12)

k = k_per(scale = 0.2, period = 1) * k_rbf(scale = 4)
m = ridge(y ~ b_ker(x, kernel = k, stdize="none"))
plot(x, y, type='l', xlab="Year", ylab="Passengers (thousands)",
    xlim=c(1949, 1965), ylim=c(100, 800))
lines(x_pred, predict(m, newdata = list(x = x_pred)), lty="dashed")